Her işin bir ehli vardır.

Örneğin; bir grafik tasarımcı ile bir ressamın işleri birbirine çok yakın gözükse de, aslında birinin yaptığı işi diğerine yaptırdığınızda aynı şey olmaktan çıkar. Kullandıkları alet-edevat bile farklılıklar gösterir. Ya da bir terzi ile bir modacı aslında aynı şeyle uğraşsalar da birbirinden çok farklı şeyler yaparlar. Modacı, terzinin üzerine birkaç özellik serpiştirilip geliştirilmiş hali gibidir, ama yine de bir şeyi onarmak söz konusu olduğunda terzinin kalıplarına uyamaz.

Bu açıdan bakıldığında bir alanda uzmanlaşmış bir kişinin diğerinin alanına müdahale ettiğinde düşebileceği durumları hayal etmek zor olmasa gerek. Bu durum özellikle “teorisyen – pratisyen” ayrımı içeren alanlarda kendisini daha çok belli eder. Modern bilimlerin yeni bir akımı olan “her şeyin içine matematik/istatistik ekleme” işine başlandı başlanalı, alan dışına çıkanların düştüğü sıkıntılı durumları sıklıkla görebiliyoruz. Çünkü bir “teorisyen” nitel gözleme dayalı varsayımlarda bulunur ve bu yolla çıkarsamalar yapar, tezler ortaya atar. İş, bu tezleri “nicel” olarak ölçmeye geldiğinde ise artık konunun dışına çıkmış olur. Çünkü bu durumda analizinin içerisine “matematik/istatistik eklemelidir”. Yani bilfiil “pratik (uygulama)” yapması gerekir.

Ekonomi alanında bu durumun en güzel örneklerinden bir tanesi “Phillips Eğrisi”dir. Phillips eğrisi, 1958 yılında İngiliz istatistikçi ve ekonomist William Phillips tarafından ortaya atılmıştır. Ortaya atıldığı günden beri de büyük tartışmalara kaynaklık etmiştir. Ücretlerin serbest bir ortamda, tam rekabet koşullarında bağımsız belirlendiği varsayımı altında, işsizlik ile enflasyonun “kısa dönemde” ters yönlü bir harekete sahip olacağını söylemektedir. “Kısa dönem” kavramının altını iki kere çizmekte fayda var çünkü ekonomideki karar vericilerin uygulayacağı anlık politikalar “kırılmalar”a yol açar ve iki grafiğin seyri bir anda değişir. “Kırılmalar” kavramının altını ise üç kere çizmek gerekir. Sebebini yazının ilerleyen kısımlarında açıklamak üzere buraya bir yıldız koyup devam edelim.

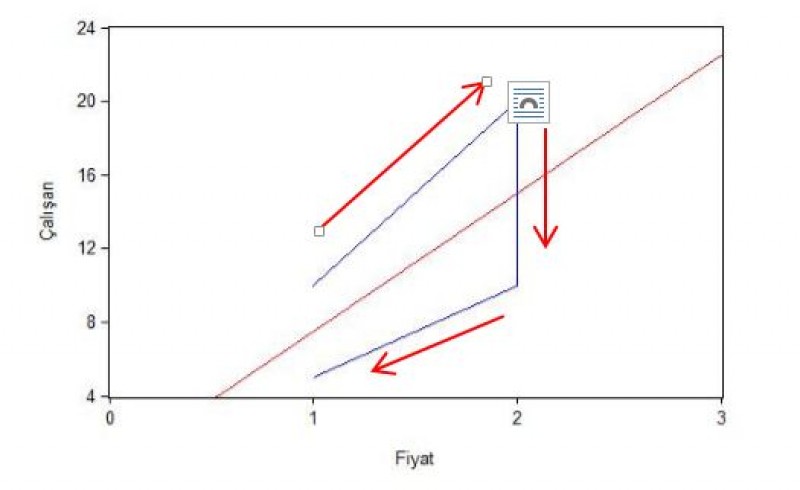
Phillips eğrisinin ne demek istediğini daha açık anlatacak olursak, piyasada satın alınacak şeylerin (örneğin üretimin ya da üretim + ithalatın) miktarının sabit olduğu durumda işsizlik azalırsa/artarsa enflasyon artar/azalır çünkü arzın miktarı sabittir ve sabit bir arz miktarına gelen talep arttığında/azaldığında satın alınacak şeylere harcanacak para yani likitide artmış/azalmış ama satın alınacak şeylerin sayısı aynı kalmış olacaktır. Sayılarla açıklayalım; piyasada 10 adet ürün olsun. Bu ürünün karşılığında ise her birinin maaşı 1 lira olan 10 çalışan olsun ve bu çalışanlardan her biri 1 adet ürün almak istesin. Bu durumda her bir ürüne karşılık 1 lira denk gelecektir. Daha sonra istihdam artsın ve bu defa her birinin maaşı 1 lira olan 20 çalışan olsun. Bu durumda artık piyasada dolaşan 20 lira vardır ve her bir ürün başına 2 lira düşmektedir. Bu durumda bir sonraki dönemde ürünün fiyatı artacak, bu da enflasyona yol açacaktır. Enflasyondaki artıştan etkilenen çalışanlar maaşlarına zam isteyecek, bu zam da yine piyasadaki para miktarını artıracak, bu da bazı durumlarda yine enflasyonla sonuçlanan başka ekonomik sonuçlara yol açacaktır ancak bu başka bir konu olduğu için parantez içinde değinip geçmekte ancak yine de ileride tekrar değinmek üzere buraya ikinci yıldızı koymakta fayda var. Çalışanlar zam alacak ancak bu zam başlangıçta yarısının, sonra onun da yarısının işinden olmasına yol açacaktır. Artık elimizde 2 lira maaş alan 5 işçi bulunmakta. Ürün sayısı sabitti yani şimdi de ürün başına düşen para 1 lira. Bu da enflasyonda düşüşe yol açmış olmakta (Lipsey’in Talep Fazlası Modeli).

Grafikteki mavi çizgi iki serinin birbirine göre hareketini, ortadaki kırmızı çizgi ise birbirleriyle doğrusal ilişkisini gösteren regresyon çizgisini göstermektedir. Buradan anlaşılan, çalışan sayısı arttıkça/azaldıkça fiyat artar/azalır, yani ilişkinin yönü aynıdır.

Basitçe bu senaryoyla açıklayabileceğimiz bir mantıkla işleyen Phillips eğrisi, açık bir şekilde iki seri için de hem birbirlerinden hem de kendilerinin bir önceki döneminden etkilenmektedir. Ayrıca görünürde bir dönem biri, bir dönem ise diğeri etkilenen değişken olmaktadır. Dolayısıyla hangisinin etkileyen olduğuna karar vermek biraz muallakta kalmakla beraber, genel akademik öğretimde ve bu yazıda uygulama yapılacak örneğin alındığı blogda etkilenen değişken olarak enflasyon alındığı için bu yazıda da aynısı yapılmıştır. “Etkileyen – etkilenen” ve “kendisinin bir dönem öncesinden etkilenen” kavramlarına da üçüncü yıldızı koyalım.

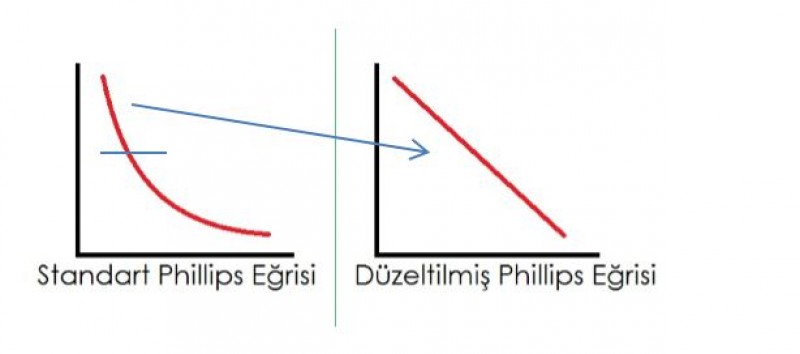
Yukarıdaki örnekte 1’e 1 bir ilişki görülmektedir ancak Phillips eğrisi teorik olarak içbükeydir. Yani bu bazı bölgelerde 1’e 0.9, bazı bölgelerde 1’e 1.1 gibi bir ilişki anlamına gelir. İki serinin ilişkisi incelenirken genellikle doğrusal analizden faydalanılır, bu sebeple teorideki Phillips eğrisi yerine “Düzeltilmiş Phillips Eğrisi” kullanılmaktadır. Düzeltilmiş Phillips eğrisinde ilişki, çizginin her nokrasında aynı eğime sahiptir yani her noktada 1’e 1’dir, standart Phillips eğrisi gibi yorumlanamaz.

Düzeltilmiş Phillips eğrisinin bir diğer kullanım amacı ise kısa dönem analizleri kuvvetlendirmektir. Standart Phillips eğrisinin uzun dönemi, düzeltilmiş Phillips eğrisinin ise standart Phillips eğrisinin bir kesitini yansıtan kısa dönemi temsil ettiği söylenir. Çünkü uzun dönemde doğrusallığı bozan ve içbükeyliğe yol açan eğim değişkenlikleri kısa dönemde görülmemektedir. İçbükey çizgi yakından incelendiğinde, bazı noktalarda denkleminde yapısal değişmeler yaşayan doğrusal çizgilerin birleşimi gibidir.

Bu kadar teorik açıklamadan sonra artık bir uygulama yapalım; farz-ı’misal elimizde Türkiye’nin 1980 - 2015 yılları arası yıllık, 2009 Ocak – 2016 Mayıs arası aylık işsizlik oranı ve tüketici fiyatları endeksini (TÜFE) içeren iki adet zaman serisi olsun. Serileri nereden elde ettiğimizin önemi yok ama illa görmek isterseniz dipnotta[1] yer alan blog sayfasındaki yazıdan edinebilirsiniz. Verilerin bahsedilen yerden alınmasının tek sebebi hem konuya örnek teşkil etmesi hem de kolay ulaşılır olmasıdır.

Doğrusal analizde genellikle “Regresyon Analizi” yönteminden yararlanılır. Bu yöntemin çeşitleri olmakla birlikte, bu çeşitlerden en çok kullanılanı ise “Standart En Küçük Kareler (SEKK) Yöntemi”dir. Regresyon analizinin çeşitlerinde seri değerleriyle birçok çizgi tahmin edilir, en küçük kareler yöntemi ise tahmin edilen bu çizgilerden tahmini bağımlı değişken değerleri ile gerçek gözlem değerleri arasındaki farkların karelerinin toplamı en küçük olanı seçer. Bunun sebebini açıklamak yazıyı uzatacağı için buraya da bir dipnot[2] şeklinde kaynak ekleyerek devam edelim.

Bahsedilen değerlerdeki serilerimizin regresyon grafiğini SEKK yöntemiyle çizecek olursak;

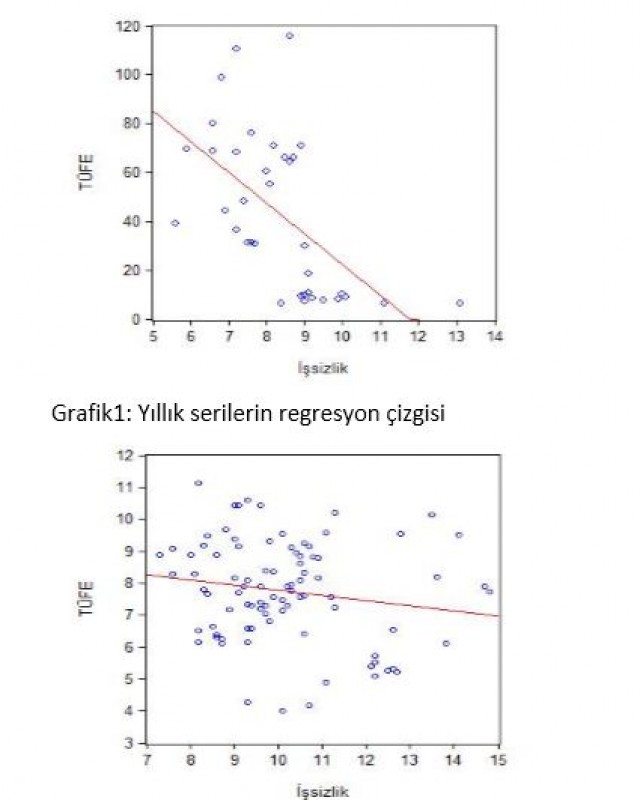
Grafik1: Yıllık serilerin regresyon çizgisi

Grafik2: Aylık serilerin regresyon çizgisi

                Çizgilerden ilki uzun dönem, ikincisi ise yine uzun dönem ama diğerine göre daha kısa dönem ilişkisini ya da yıllık bazda kısa dönem, aylık bazda ise uzun dönem ilişkiyi göstermektedir. İki regresyon analizinde de enflasyon ve işsizlik arasında ters yönlü bir ilişki olduğunu görüyoruz. Yani Phillips eğrisinin teorisini destekleyecek iki adet “çizgi” var elimizde. Ancak üzülerek ifade etmeliyim ki yorumlama açısından iki analizin de cetveli elimize alıp noktaların arasından rastgele geçirdiğimiz çizgilerden hiçbir farkı yok!

                Eğer bu şekilde bir çalışma yapıp raporlasak, bu hata yetmezmiş gibi üstüne bir de bu raporu birilerine sunsak, çok kritik hatalarla dolu bir analizi “yutturmaya çalışmak”tan daha öte bir şey yapmış olmayız, her ne kadar iyi niyetli olsak da maalesef ki gerçek bu. “Phillips eğrisinin teorisi”ni anlatan bir ekonomistin işi orada biter, sonrası ekonometristin işidir.

Peki neden?

Öncelikle, eğer SEKK yöntemini uyguluyorsanız “varsayımları” olduğunu bilmelisiniz. Bu varsayımlar küçük örneklem / büyük örneklem ayrımına sahiptir ve bunlarda farklı özellikler gösterir. Özellikle küçük örneklem söz konusu ise, analizinizde eğer bu varsayımlardan birisi bile geçersizse yani tutmazsa, analizinizin güvenilirliğini sorgulamaya başlamalısınız.

Tüm varsayımlar geçerli diyelim, bu sefer de regresyon doğrusunun denkleminin ve bu denklemin katsayılarının istatistiksel anlamlılığı sınanmalıdır, belirginliği yani ilişkiyi açıklama oranı görülmelidir. Bu şekilde kurduğunuz modelin doğruluğu konusunda bir fikir edinir ve daha doğru bir açıklayıcı ilişki kurmuş olursunuz.

Yukarıdaki iki konuda hiçbir sorunla karşılaşmadınız diyelim. Yine de şu kritik hatayı yaptınız; teoride doğrusal olmadığı söylenen bir uzun dönem ilişkiyi sabit eğimli çizgiyle açıkladınız!

Bu durumu şöyle bir örnekle açıklayalım;

Bir regresyon analizinde regresyon çizgisinin etrafındaki noktaların çizgiye uzaklığının her yerde aşağı yukarı aynı olması beklenir. Bu SEKK’in varsayımlarından “sabit varyans”tır.

https://en.wikipedia.org/wiki/Linear_regression

Eğer sabit varyans varsayımı geçersizse, analiz birçok sebepten geçerliliğini yitirir.

Beta katsayısı, regresyon denkleminin eğimidir. Etkileyen değişkendeki 1 birimlik değişimin etkilenen değişkene ne kadar yansıdığını gösterir. Sabit varyanslı dağılıma sahip bir gözlem aralığının regresyon denklemindeki beta katsayısının eğiminin, gözlemlerin daha küçük aralıklarının tümünde birbirine çok yakın ve aynı işaretli eğime sahip olması beklenir. Yani gözlemlerin birinci ve onuncu değerleriyle kurulan regresyonun eğimi, dokuzuncu ve ondokuzuncu gözlemleriyle kurulan regresyonun eğimiyle aynı işarete sahip ve değer olarak birbirine çok yakındır. Eğer dönem dönem beta katsayısında işaret değişikliği ve büyük değer değişikliği oluyorsa, bu analizde değişen varyans varlığından şüphelenmeye başlamak gerekir.

Şimdi kendi verilerimize dönelim ve bu uygulamayı “Hareketli Regresyon[3]” yöntemiyle elde edilen dönemlik katsayılar üzerinde görelim.

Grafik 3’te yıllık işsizlik ve enflasyon serilerimize uygulanmış hareketli regresyon sonucu elde edilen 5 yıllık ve 10 yıllık beta katsayıları görülmektedir.

Beta katsayılarındaki değer ve işaret değişimleri gözle görülür şekilde büyüktür. Zaten daha yukarı gidip Grafik 1 ve 2’den serilerin dağılımına bakarsak, aykırı değerlerin[4] ve varyanstaki değişimin ne kadar bariz olduğunu görmek mümkün.

Bir de aylık seriyi inceleyelim. Grafik 5’te 24 aylık, Grafik 6da ise 48 aylık yuvarlanan regresyon denkleminin beta katsayılarındaki değişim görülmektedir.

Elimizdeki gözlem aralığını daraltıp ilerlettikçe, ilişkinin nasıl şekil değiştirdiğini görmektesiniz. Oysa ki beta değerlerinin bazı dönemlerde sıfırın üstüne çıkması pek de beklemediğimiz bir durumdur. Beta katsayısı sıfırın üstüne çıktığında, etkileyen değişkendeki 1 birimlik artış, etkilenen değişkende de aynı yönlü bir artışa yol açacaktır. Oysa bizim genelde beklediğimiz etkileyen değişkendeki 1 birimlik değişime karşılık etkilenen değişkende azalıştır ya da tam tersi.

Teknik açıklamaları daha da uzatıp karmaşıklaştırmamak için buradaki konuyu dipnotlarla geçiştirmek gerek, yoksa kafamıza göre “bu aykırı değerdir”, “bu seride aykırı değerler vardır” ya da “beta katsayıları çok değişkense değişen varyans vardır” demek de mümkün değil, hepsinin kendine ait ayrı bir matematiksel yöntemle incelenip açıklanması gerekir. Bu örneklerin maksadı konunun mantığını açıklamaktır. Burada amaç, ilişkinin, ele alınan dönem aralığına göre nasıl şekil değiştirdiğini anlatmaktır. Buradan yola çıkarak, dönemsel değişkenlikleri ve dalgalanmaları hesaba katmadan analiz yapmak, noktaların arasına cetvelle nizami bir çizgi çekmekten farksızdır çünkü yukarıda da belirtildiği gibi beta katsayılarında dönem aralıklarına göre bu denli büyük ve zıt değişimlerin olması beklenen ve istenen bir durum değildir. Aynı zamanda burada kısa dönem – uzun dönem aralığı nedir sorusuna da akademik olarak kabul görmüş skalayla karar vermek gerekmektedir. Bu da analizin geçerliliğini sağlayacak temel unsurdur.

 Buraya kadar regresyon çizgisinin neden bu şekilde çizilemeyeceğinin ekonometrik açıklamasını yaptık. Buradan sonra da kısaca direk ekonomi teorisine değinelim.

Phillips eğrisinin ilk hali İngiltere’de 1861-1913 ve 1913-1957 dönemlerindeki “parasal ücretlerdeki değişimi” ile “işsizlik oranı” arasında kurulmuştur. “Parasal ücretlerdeki değişim” yerine “enflasyon oranı”nı 1960 yılında “Samulsen ve Solow” yerleştirmiş, bundan sonra Phillips eğrisi makroekonomik analizlerde popülerlik kazanmıştır. Ancak daha sonra Friedman ve Phelps’in eleştirileriyle, eğrinin istikrarı sorgulanmış ve değişen enflasyon beklentilerinin hesaba katılarak Phillips eğrisinin ilerleyen dönemlerde kaymalar yaşadığı yeni teori oluşturulmuştur. Friedman ve Phelps kısa dönemli Phillips eğrisinin istikrarlı olması bir yana, uzun dönemde enflasyon ve işsizlik oranı arasında negatif (zıt) yönlü bir ilişki (değiş-tokuş) dahi olmadığını öne sürmüşlerdir. “Adaptif beklentiler varsayımı” ile enflasyon oranı üzerindeki beklentilerin gerçekleşen enflasyondaki artışa karşılık arttığı kabul edilmiştir. Bu da kısa dönemde Phillips eğrisini sağa ya da sola kaydıracak, beklenen enflasyon oranlarına göre alternatif Phillips eğrilerinin oluşmasına yol açacaktır. Dahası, adaptif beklentiler varsayımı, çeşitli ilişki açıklamalarıyla uzun dönemde Phillips eğrisinin “doğal işsizlik oranı”na yani enflasyon ne olursa olsun var olan işsizliğe eşit olacağını, dolayısıyla x eksenine dik düz bir çizgi şeklinde olacağını söylemektedir.

Bu kısa iktisat teorisini okuduktan sonra, yukarıdaki verilerle çizilen çizginin ne kadar da yanlış olduğunu anlamak bir kez daha mümkün olsa gerek. Aynı zamanda beta katsayılarındaki istenmeyen değişimin daha iyi anlaşılması için de bir kapı aralamış olacak. Kaldı ki, bu teoriler, teorisyenleri tarafından bile yetersiz ve gerçek veriler üstündeki açıklayıcılığına pek de güvenilmeyen teoriler olarak görülmüş, kısa dönemde daha iyi açıklamalar verse de uzun dönemde güvenilmez olduğu genel kabul görmüştür. Teori ancak kendi varsayımları ve senaryolarında tam geçerlidir, gerçek verilerde ise bu uyumu yakalamak çoğunlukla mümkün olmamaktadır. Her senaryo gibi bu senaryolar da bazı durumların kalıplara oturtulup mantıken açıklanmasından ibarettir.

Yani demem o ki, “şu ülkede şu kadarlık uzun bir dönemde enflasyon ile işsizlik arasında değiş tokuş vardır” demek pek de mümkün değildir.

Peki hem teoride hem de pratikte bu kadar fazla sorun varsa, bunların bir çözümü yok mu?

Elbette her sorun beraberinde bir çözümü getirir (İlk kısımlarda yer alan analizi yapan birisi daha sorun açıklamalarına bile gelememiş olacağı için buradan sonrası biraz ileri aşama olacak).

Çözümlere başlamadan şunu ifade etmeliyim ki, buraya gelene kadar gördüğünüz tüm grafikler ve çiziliş yolları tamamen “uydurmadır” ve uydurukluğunu anlatmak üzere yer verilmiştir. Bunun sebebini buradan sonraki kısımlarda anlamanız mümkün olacak.

Bir seri üstünde yapılacak matematiksel ve istatistiksel analizlerin en başında “durağanlık” gelir. Durağanlık, incelenen serilerin ortalamasının ve varyansının bazı sebeplerle dönemsel değişikliklere uğramadığı ve iki dönem değerlerinin ortak varyansının zamana değil, iki değerin birbirine uzaklığına bağlı olduğu yani zaman geçtikçe bir değerden öbürüne gittikçe dağılımın varyansında bir değişim olmadığı, değerlerin ortak varyansının iki değerin yer aldığı dönemdeki farka bağlı olarak belirlendiği anlamına gelir. Durağan olmayan bir seri kalıcı şoklara, aşağı veya yukarı yönlü bir eğime (trende), mevsim etkisine ya da dönem dönem alçalıp yükselen bir konjonktürel dalgalanmaya sahip olabilir[5]. Bu sebeple seri bu değerlerden arındırılmadan üzerinde analiz yapmak “sahte regresyon” sorununa yol açacaktır. Serilerimizdeki durağanlığı “birim kök[6]” testleriyle sınarız ve varlığına ya da yokluğuna karar veririz ki bu kavrama üçüncü yıldızı koymuştuk.

Kendisinin bir ya da birkaç dönem öncesinden etkilenen değerlerden oluşan serilerin varyansı zamanla genişler veya daralır. Seri değerleri tıpkı akan bir suya atılmış gül yaprakları gibi sağa-sola genişleyerek, aşağı yukarı rastgele hareketler yaparak ilerler gibidir. Burada “otoregresif modellere” değinmeden edemeyeceğim. Bu modellerden bir yöntem türetip geniş finansal serilere uygulayan Engle ve Granger 2003 yılında Nobel Ekonomi Ödülü almışlardır. Bu isimlerden Clive Granger ileride değineceğimiz  “Eşbütünleşme Analizi”nin mucididir. Bu iki kafadar, 80lerden önce yapılan serilerin neden geçersiz olduğunu açıklayan geniş bir çalışmanın da sahibidir[7].

80’lerden önce yapılan analizlerin (ne yazık ki bu tür analizler yukarıda da görüleceği gibi hala yapılmaktadır) geçersizliğinin sebeplerinden birisi de “sahte regresyon”dur. İlk kez Yule tarafından 1926 yılında öne sürülmüştür. 1958’den çok önce olmasının garip bir ironi olduğunu düşünmek olağan olsa gerek. Bu kavram üstüne yapılan çalışmalarda yine ekonomik analizlerin yaramaz çocuğu Clive Granger’i görüyoruz. Kendisi, Newbold ile 1974 yılında bir çalışma yapmış ve geniş açıklamalara yer vermiş.

Durağan olmayan serilerin içerdiği kendisine ait olmayan etkiler, aralarında doğrusal bir illişki varmış gibi görülmesine sebep olmaktadır. Bu durumda regresyon doğrusunun açıklayıcılığı (R2), gözlem değerleriyle regresyon doğrusunu çizen tahmini değerler arasındaki fark değerlerinin birbirlerinin önceki değerlerinden etkilenip etkilenmediğini (bu da SEKK’nın bir diğer varsayımı olan “otokorelasyon”dur) araştıran istatistik değerinden (Durbin-Watson d) büyük olmaktadır (Granger ve Newbold’un 1974 yılındaki çalışmasından).

Analizin güvenilirliğini sarsan ve geçerliliğini ortadan kaldıran durumlardan birisi de “yapısal kırılmalar”dır ki buna da ilk yıldızı koymuştuk. Yapısal kırılma kavramına 1954 yılında E. S. Page tarafından geliştirilen CUSUM testiyle bir kapı aralanmış ancak tam manasıyla 1960 yılında Gregory Chow tarafından geliştirilen yapısal kırılma testinde görülmüştür. “Yapısal kırılma” kavramını popüler hale getiren ise David Hendry olmuştur. Kavramı kısaca açıklayacak olursak, doğrusal regresyon çizgisi çekilmiş iki değişkenin ilişkisi, analiz dönemi içerisinde bir yapısal kırılmaya uğrar ve bu kırılma noktasından önce ve sonra farklı denklemlere sahiptir.

Yapısal kırılma kavramı daha sonra 1989 yılında Perron’un serilerin durağanlığı üstüne yaptığı çalışmalara konu olmuş, Perron daha önceleri yapılan durağanlık analizlerinde durağan olmadığı tespit edilen serilerin aslında yapısal kırılmalar geçirmiş durağan seriler olduğunu tespit etmiştir.

Peki yapısal kırılmalar neden gerçekleşir? Anlık veya dönemlik bir politika değişikliği, kriz, anlık fiyat değişikliği ve bunun etkisinin devam etmesi, çevresel etkilerden kaynaklanan anlık olayların etkisi sonucu davranış değişikliği, vb. İşte bu sebeplerle, kısa dönemlerde yapılan analizler uzun dönemi yansıtmamaktadır.

Aslında sorunlara üretilen çözümlerden önce açıklanması gereken bir dizi sorun daha var ama bu sorunlara kısaca değinmekle yetinelim. Örneğin kullandığınız istatistiki yöntemlerin tümü bir istatistiki dağılıma uyduğu için ve regresyon analizinin varsayımlarından birisinin de “normallik (kalıntılarda)” olduğu düşünülürse, elinizde bir normallik sınaması olması gerekir. Yine varsayımlardan birisi “model kurma hatası yapılmamıştır” olduğu için, bir de “model seçim analizi” eklemekte fayda var. Bu analizlerin her birinin sonucu, varsayımlardan birisinin geçerli olduğunu, dolayısıyla analizin geçerliliğini göstermektedir. Değişen varyans ve otokorelasyon sınamalarına da daha önce değinmiştik. Değinilmeyen başka sınamalar da bulunmakta. Buradan şunları anlamak mümkün;

Her teorinin bir varsayımı vardır ancak işin içine matematiği kattığınızda teorik varsayımlar uygulamalı olarak geçerlilik sınamasına sokulmalıdır. Kısacası “kafanıza göre regresyon çizgisi çizemezsiniz”.

Üzerinde çalıştığı teoriye saygısı olan birisi, teoriyi ispat etmek için hem kendi teorisinin hem de onu ispatlamak için kullandığı yöntemlerin varsayımları gibi içeriklerini çiğnemez. Eğer öyle olmasaydı bunca yöntem üretilmezdi.

İşte sayılan bu sebeplerle güvenilirliği sorgulanan uzun ve kısa dönem analizler için güvenilirliği artırıcı çözümler üretilmiştir. Sayacağımız ilk çözümde karşımıza yine Clive Granger çıkıyor.

Clive Granger, 1969 yılında geliştirdiği “Nedensellik Analizi” ile, bir serinin diğerini açıklamada yeterli olup olmadığını tespit edecek bir yöntem öne sürmüşlerdir. Yani enflasyon ile işsizlik serileri arasında bir analiz yapmak istediğinizde, hangisinin etkileyen hangisinin etkilenen olduğunu bu yöntemle tespit etmeniz mümkün.

Diğer bir çözüm ise daha önce de bahsedilen “Eşbütünleşme Testi”dir. Bu yöntemle durağan olmayan iki zaman serisi arasındaki ilişkinin varlığı incelenebilir. Son dönem analizlerinde oldukça popülerdir ve sürekli de gelişmekte. Hatta geleneksel istatistiki dağılımları yok sayıp kendi dağılımlarını üretenler bile çıkmaya başladı.

Bu testler yapıldıktan sonra elimizde bir denklem olmasını isteyebiliriz. Bunun için de “modifiye edilmiş ve dinamik en küçük kareler” ve “Gregory-Hansen eşbütünleşme testi” yöntemleri örnek gösterilebilir. Bu ve benzeri yöntemlerle, doğrusal ilişkiden uzaklaşan gözlemlerin ne kadar süre sonra doğrusal ilişkiye yöneldiği, katsayı olarak analize dahil edilir (Tabi ki eşbütünleşik serilerde).

Çözümlere çok kısa değindik çünkü detaylı açıklamaya kalkarsak bu yazının sonuna bir de lisans ya da yüksek lisans diploması eklemek gerekebilir. Umulan odur ki, bahsedilen bu çözümlerin bire bir uygulamasını Phillips eğrisi teorisi üstüne detaylı bir şekilde ikinci yazıda yapalım.

Edmund Phelps, Phillips eğrisini çürüten bir çalışma yapmış, bu çalışmayla 2006 yılında Nobel ödülü almıştır. İki soyismin benzerliği sizin de dikkatinizi çekti mi?  Koopmans, Phillips eğrisini “teorisiz ölçüm” olarak niteler. Bu yazıda ise tam tersi iddia edilmektedir. Çünkü Phillips eğrisi başta “ceteris paribus[8]” olmak üzere bir iktisat teorisinin gerektirdiği her noktayı barındırır, her değişim ve gelişim sürecini geçirmiştir. “Ceteris paribus”un altını çizmek gerek, nitekim teoride sabit olan diğer etkenler gerçek hayatta sabit değildir. Analiz yapılan seriler teoride sabit olması gereken tüm diğer etkileri içerir, burada ikinci yıldızı hatırlatalım. Ekonomik verilerin tamamı türlü döngüler, ilişkiler ve etkiler içerir. Her bir veri birkaç diğerinin etkisiyle şekillenir, bununla birlikte şekillendirdiği değerlerden de etkilenir. Uzun dönemde istenilen sonucu vermemesinin, kısa dönemde ise daha iyi sonuçlar verdiğinin düşünülmesinin altında bu sebep yatmaktadır. Phillips eğrisinin bir versiyonu çürütüldüğünde yerine yeni bir versiyonu konulmuş. Bazıları[9];

Uyarlanabilir Beklentiler ve Phillips Eğrisi: Monetarist Görüş

Rasyonel Beklentiler ve Phillips Eğrisi: Yeni Klasik Görüş

Yarı Rasyonel ve/veya Rasyonel Beklentiler: Yeni Keynesyen Görüş

Heterojen Beklentiler: Post Keynesyen Görüş

Yani teorisyenler kendi içlerinde bu konuyu tartışıp şekil değiştirtmişler ve günümüzdeki çözümlere kadar ulaşmışlardır ki normal bir bilimin işleyiş süreci de bunu gerektirir. Dolayısıyla, bu kadar evre atlanmışken hala en baştaki konumda çalışmalar yapmak ancak bir öğrenci için kabul edilebilir, akademisyenlikle ya da bilim insanlığıyla zerre kadar alakası yoktur.

Sonuca gelecek olursak, bu kadar uzun ve nispeten fazla teknik açıklamalar yapılmış bu yazının özeti şudur; eğer birisi size tek işlemden oluşan teori ispatı yaparsa inanmayın. Örneğin yukarıdaki gibi bir ilişki açıklamasına rastlarsanız okumaya dahi tenezzül etmeden geçin ki belki yazarın yıllarca uğraşıp aldığı bir ünvanı vardır, gözünüzde o ünvanın getirdiği saygınlığı yitirmesin. Hele ki o tür analizlerle politik, sosyal, finansal çıkarımlarda kesinlikle bulunmayın, bulunursanız %99 yanılırsınız. %l’lik payı “Bozuk saat bile günde iki kere doğruyu gösterir” deyişine hürmeten bıraktım.

Yazının sonuna bu konuda yapılmış birkaç çalışma önerisi eklemek isterim. Belki yukarıda anlatılanlara daha iyi bir açıklayıcı olur;

Phillips Eğrisi: Yarım Yüzyıldır Bitmeyen Tartışma – Tahir Büyükakın

Türkiye’de Phillips Eğrisi Üzerine Bir Uygulama – Metin Bayrak / Osman Cenk Kanca

Yeni Keynesyen Bakış Açısıyla Türkiye’nin Enflasyon Dinamikleri Yönünden Yapısal Analizi – Ferhat Çamlıca